Quantum harmonic oscillator
The quantum harmonic oscillator is a fundamental model in quantum mechanics due to its wide applicability in physics, from simple models of atoms to quantization of fields in quantum field theory. The oscillator's energy levels are quantized, and this can be elegantly described using ladder operators.
First, consider the time-independent Schrödinger equation for the harmonic oscillator:
$$ \hat{H} \psi(x) = E \psi(x) $$
where $\hat{H}$ is the Hamiltonian operator:
$$ \hat{H} = \frac{\hat{p}^2}{2m} + \frac{1}{2} m \omega^2 \hat{x}^2 \tag{1}$$
and $\hat{p}$ and $\hat{x}$ are the momentum and position operators, respectively.
The ladder operators $\hat{a}$ and $\hat{a}^\dagger$ (annihilation and creation operators, respectively) are introduced as:
$$ \hat{a} = \sqrt{\frac{m\omega}{2\hbar}} \left( \hat{x} + \frac{i\hat{p}}{m\omega} \right), \quad \hat{a}^\dagger = \sqrt{\frac{m\omega}{2\hbar}} \left( \hat{x} - \frac{i\hat{p}}{m\omega} \right) $$
These operators lower and raise the energy levels of the oscillator, respectively. They obey the commutation relation $[\hat{a}, \hat{a}^\dagger] = 1$.
Using ladder operators, the Hamiltonian can be rewritten as:
$$ \hat{H} = \hbar \omega \left( \hat{a}^\dagger \hat{a} + \frac{1}{2} \right) $$
This form is particularly useful as it manifests the quantization of the oscillator’s energy directly.
Now, for the existence of a ground state: if we apply the annihilation operator to an eigenstate of the Hamiltonian $\psi$ with energy $E$, the resultant state $\hat{a} \psi$ is an eigenstate with energy $E - \hbar \omega$. Conversely, applying the creation operator $\hat{a}^\dagger$ to $\psi$ yields a state with energy $E + \hbar \omega$. This implies that we can construct a "ladder" of energy states by repeatedly applying $\hat{a}^\dagger$ or $\hat{a}$. These two facts can be checked by computations.
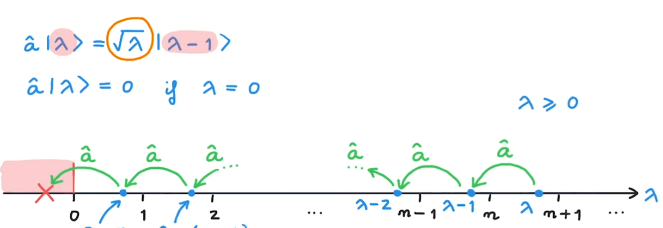
Crucially, the energy cannot be negative, according to $(1)$, so there must be a lowest energy state such that further application of $\hat{a}$ yields zero. This state $| 0 \rangle$, satisfying $\hat{a} | 0 \rangle = 0$, is the ground state. It has the energy $E_0 = \frac{1}{2} \hbar \omega$, which includes the zero-point energy, the non-zero energy that the oscillator possesses in the ground state due to the Heisenberg uncertainty principle.
This can be shown in another form by defining the number operator $\hat{N}=\hat{a}^\dagger \hat{a}$. The eigenstates of $\hat{N}$ are the same as the eigenstates of $\hat{H}$. Let's call them $|\lambda\rangle$, for every eigenvalue $\lambda$. Now observe that
$$ \langle \lambda | \hat{N} | \lambda \rangle = \lambda \langle \lambda | \lambda \rangle = \lambda $$and
$$ \langle \lambda | \hat{N} | \lambda \rangle = (\langle \lambda | \hat{a}^\dagger)(\hat{a} | \lambda \rangle) = || \hat{a} | \lambda \rangle ||^2 \geq 0 $$from where we conclude $\lambda \geq 0$.
Why Discrete Energy Levels:
see this video.
Time evolution of energy eigenstates and coherent eigenstates
Energy eigenstates: Schrodinger equation.
Coherent states:
The eigenstates of the annihilation operator, $\hat{a}(|\alpha\rangle)=\alpha |\alpha\rangle$, where $\alpha \in \mathbb C$, are called coherent states. Their time evolution is given by
$$ \begin{aligned} & |\psi(0)\rangle=\left|\alpha_0\right\rangle \quad \alpha_0=\left|\alpha_0\right| e^{i \varphi} \\ & |\psi(t)\rangle=e^{-i \omega t / 2}|\alpha\rangle, \text{ where } \alpha=\alpha_0 e^{-i \omega t} \end{aligned} $$(see this video
Comparison with classical
| Description | Classical Harmonic Oscillator | Quantum Harmonic Oscillator (initial Coherent State $\alpha_0$) |
| Position $x(t)$ | $x_0 \cos(\omega t - \varphi)$ | $\sqrt{\frac{2\hbar}{m\omega}} \|\alpha_0\| \cos(\omega t - \varphi)$ |
| Momentum $p(t)$ | $-m\omega x_0 \sin(\omega t - \varphi)$ | $-\sqrt{2m\hbar\omega} \|\alpha_0\| \sin(\omega t - \varphi)$ |
| Energy $E(t)$ | $\frac{1}{2}m\omega^2 x_0^2$ | $\hbar\omega \left( \|\alpha_0\| ^2 + \frac{1}{2}\right)$ |
The energy for the quantum case includes the contribution from the zero-point energy $\frac{1}{2}\hbar\omega$, which is absent in the classical case.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: